
Joseph Louis Lagrange
definition on Wikipedia:
In mathematical optimization, the method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function subject to equality constraints. (Wikipedia)
拉格朗日乘子法 是一种在一个或多个约束条件下,局部最小化或最大化函数的方法。
例如:对变量 $x$ 和 $y$ 使 $x^2 + y^2$ 尽可能小,同时满足约束$xy = 1$。
以下是如何使用拉格朗日乘子法及其工作原理的解释:
这个解释(尤其是为什么它们的工作)只有一个约束要简单得多,所以我们将从一个直观的论证开始,然后在多个约束的情况下转向一个更严格的论证。这两种情况都需要熟悉偏导数和向量
一个约束条件
假设我们想要根据约束 $g(x, y) = 0$, 最小化函数 $f(x, y)$ 。
(现在我们将最小化两个变量的函数,但是该方法将自然地扩展到更多变量的函数,并且最大化的过程完全相同。)
对于上面的例子,$f(x, y) = x^2 + y^2$ 和 $g(x, y)=xy-1$ (因为 $xy - 1 = 0$ 等价 $xy = 1$ )。
为了解决这个问题,我们创建了一个 $L(x, y, \lambda)$ 名为 Lagrangian 的新函数。
它被定义为 $L(x, y, \lambda)= f(x,y) - \lambda g(x, y)$ ,其中 $\lambda$ 是一个称为拉格朗日乘子的新变量。
(有些人用 $+$,而不是 $-$ ,但这并没有改变定义,除了$\lambda$的符号发生变化。)
然后,我们取原始变量$x$ 、 $y$、 $\lambda$ 相对于 $L$ 的偏导数,将所有这些部分设置为零,并求解 $x$ 和 $y$ 。
对于上面给出的例子,我们有:
将所有部分设置为零并求解,我们得到它 $\lambda = 2$ 并且(x, y)是(1, 1)或者(-1, -1)。
实际上,这些点是受制于约束 $g(x, y) = 0$的 $f(x, y)$ 局部最小值。(在这种情况下,它们也是全局极小值,虽然通常不能保证。)
引言
为什么拉格朗日乘子法有效?
人们很容易认为我们可以通过找到一个不受约束 $L$ 的最小值, 来找到一个受约束的 $f$ 的最小值; 毕竟,我们将所有 $L$ 的分量设置为等于零。但这是错误的。解决方案 $(x, y, \lambda)$ 实际上,从来不是局部最小值或最大值,总是会有一个马鞍点对应到 $L$。那么为什么拉格朗日乘子法有效呢?答案与等高曲线和梯度有关。
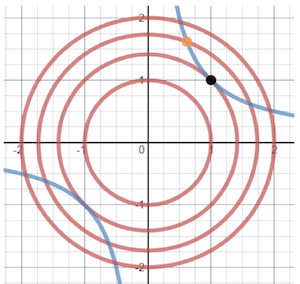
等值曲线
函数的等值曲线[等高线]是函数等于常数值的点集。
(在三个维度中,它们被称为等值面,更一般地说,等值集合。)
在上面的图片中,红色圆是一些等值曲线 $f(x, y) = x^2 + y^2$(较大的圆对应于 $f$中更高的值)。
蓝色曲线是满足约束 $g(x, y) = 0$ 的点集,使其成为 $ g(x, y)$ 的一条等值曲线。
几何分析
约束最小化就是寻找蓝色曲线上红色谷中最低的点:每个红色曲线代表不同高度的谷。
事实证明,这极值点总是红色和蓝色等值曲线的相切点,例如上图中的黑点。
要了解原因,有必要查看曲线不相切的点,例如橙色点。由于红色和蓝色等值曲线在橙色点彼此不相切,它们彼此交叉。由于它们交叉,当沿着蓝色曲线在红色谷中向一个方向上移动时,红谷值向另一个方向移动向下移动。
换句话说,存在局部变化 $(x, y)$,在保持约束 $g(x, y) = 0$ 的情况下,导致目标函数$f(x, y)$减少,而相反的变化导致它增加。 因此交叉点不可能是受限制的最小值或最大值。由于最小值不能在等值曲线交叉的点处,因此它必须在它们相切的点处。在切点,当你沿着曲线 $g(x, y) = 0$ 移动时, $f(x, y)$ 是近似不变的一阶导数,因此它可能是最小值或最大值。(它可能也不是,但至少它可能是。)
数学分析
我们如何在数学上表达等值曲线 $f$ 和 $g$ 相切?这是梯度的来源。函数的梯度 $f$ 被写为 $ \nabla f$ 并定义为向量,其中每个分量是 $f$ 相对于相应变量的偏导数:$\nabla f = (\partial f / \partial x, \partial f / \partial y)$。梯度具有对我们非常有用的属性:$f$ 的梯度总是垂直于 $f$ 给定的等值曲线$(x, y)$。要探究这个问题,我们定义 $(\Delta x, \Delta y)$ 是改变$(x, y)$的微元[small amount]。它将如何改变f$(x, y)$?首先,答案是:
如果$(\Delta x, \Delta y)$是在等值曲线的方向,我们将拥有 $ f(x + \Delta x, y + \Delta y) \approx f(x, y)$,这意味着 $\frac{\partial f}{\partial x}\Delta x + \frac{\partial f}{\partial y} \Delta y = 0 $ 。换句话说,$\nabla f$ 和 $(\Delta x, \Delta y)$ 的点积为零。由于 $(\Delta x, \Delta y)$在等值曲线的方向上,这意味着 等值曲线和梯度彼此垂直。
由于我们希望的等值曲线 $f$ 和 $g$ 为彼此相切,并且每个函数的梯度是垂直于它的等值曲线中,我们希望梯度以在相同的方向(或沿相反方向)指向。如果一个是另一个的标量倍数,则两个向量指向相同的方向。 这个标量将成为拉格朗日乘子,我们称之为$ \lambda: \nabla f = \lambda \nabla g$。该向量方程扩展为每个 $x$ 和的一个方程 $y$。将约束本身添加到我们的方程组中,我们得到:
\begin{array}{rcl}\frac{\partial f}{\partial x}&=&\lambda \frac{\partial g}{\partial x}\ \frac{\partial f}{\partial y}&=&\lambda \frac{\partial g}{\partial y} \ g(x, y) & = & 0 \end{array}
小结
Lagrange multipliers方法就是产生这些方程并求解它们。然而它通常用拉格朗日函数来描述 $ L(x, y, \lambda) = f(x, y) - \lambda g(x, y)$。将 $x$, $y$, $\lambda$ 关于Lagrangian的偏导数,写成以上例子的形式。例如,$ \partial L / \partial x = \partial f / \partial x - \lambda \partial g / \partial x$。 将这个值设为零就可以得到例子中的第一个方程。最后还有一个等式,$ \partial L / \partial \lambda = -g(x, y)$。如果你愿意,你根本就不需要担心Lagrangian,你只需要找到一个点$(x, y)$ 和标量 $\lambda$,使$ \nabla f = \lambda \nabla g$ 满足约束条件。这些点将是约束最小值(或最大值)的候选值。
总之,约束极小值和极大值出现在约束函数的等值曲线 $g$与 目标函数的等值曲线 $f$的相切的点处。
当 $ \nabla f = \lambda \nabla g$ 时,有以上例子中的方程式成立。拉格朗日函数$L$用一个函数的偏导数将这些方程统一起来。
后记
在切点位置两等值曲线方向平行,考虑到梯度和等值曲线垂直,那么可以用梯度平行来求切点位置。
切点 -> 变量偏导比例相等 -> 梯度方向相同 -> 梯度模成比例 -> 候选极值
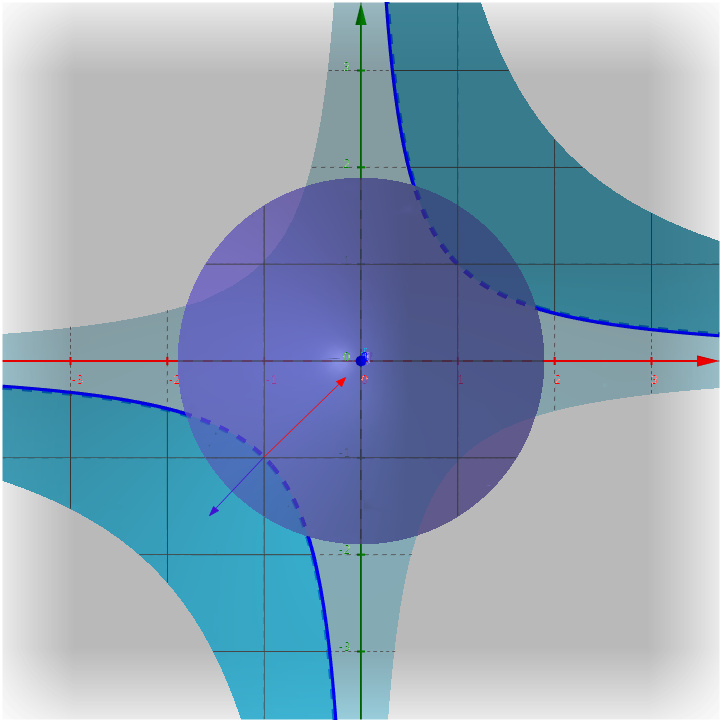
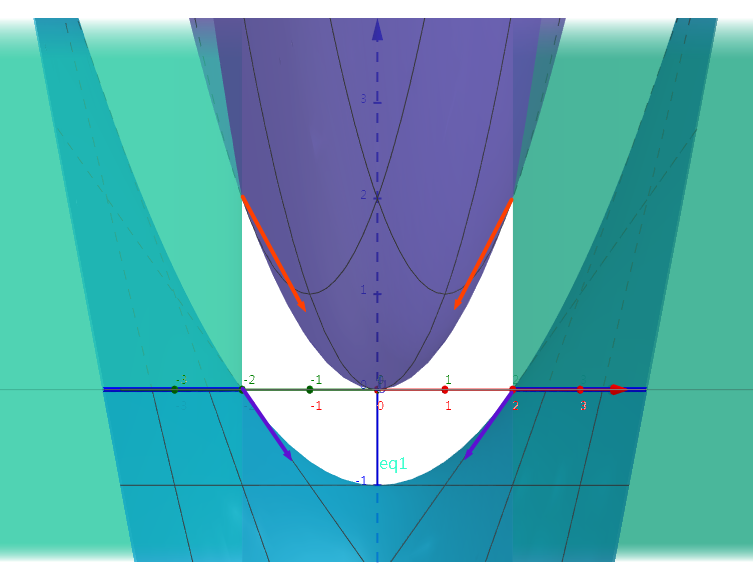
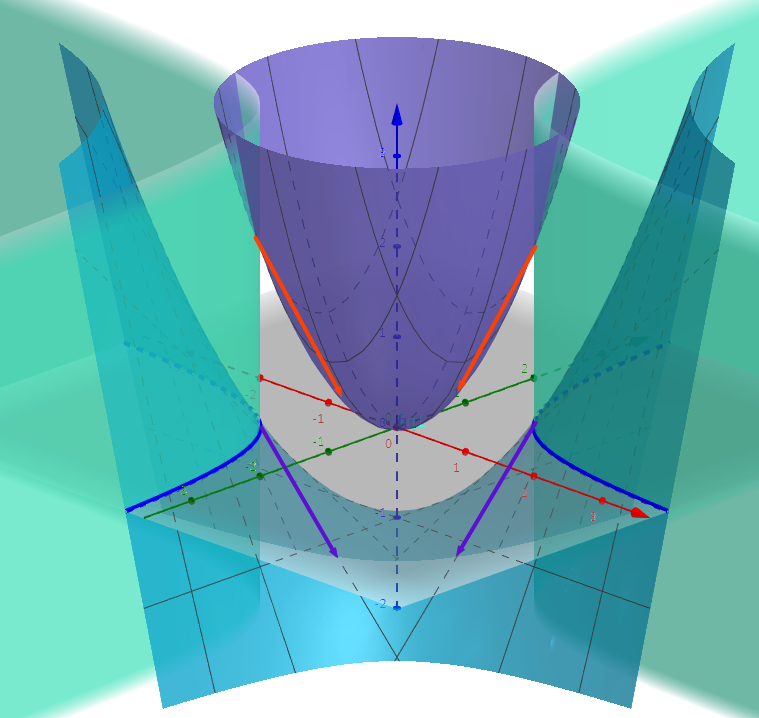
https://danstronger.wordpress.com/2015/08/08/lagrange-multipliers/
https://jermmy.github.io/2017/07/27/2017-7-27-understand-lagrange-multiplier/
https://www.svm-tutorial.com/2016/09/duality-lagrange-multipliers/